Geometrie trysky, teorie a výpočetní příklady

Ahoj,

abych to ještě více rozšťoural, mám tady další výpočet a to hybridního motoru:

Jako palivo použijeme ABS (Akrylonitril Butadien Styren), okysličovadlo bude (kupodivu) N_ěO.

Jako ideální směšovací poměr vychází O/F=6,4
I_s je tady už velmi zajímavé a to 229 s.

Přeskočíme problém, jak tohoto impulsu dosáhnout a podíváme se na trysku

Jako ideální nám vychází A_e/A_t = 5,4 (340 m n.m.)
Výtoková rychlost v_e=2386 m/s.

Pro A_e/A_t = 2,5 vychází v_e = 2043 m/s. Rozdíl je 17%.

A teď pohled z mírně jiného pohledu. V příloze je výkres tří trysek týkajících se dříve probíraného sorbitolového motoru.
Tryska 1 - tryska s kompletní expanzí A_e/A_t = 5,7. Vyrobena z oceli má hmotnost 88 gramů. Je pro motor zhruba průměru 50 mm, zajištění ségrovkou, těsnění O-kroužkem. Délka trysky a tedy i polotovaru je cca 40 mm.
Tryska 2 - tryska s A_e/A_t = 2,5. Hmotnost 70 gramů. Je výrazně kratší, 25 mm.
Tryska 3 - tryska s A_e/A_t = 2, hodně zkrácená, na 14 mm. Hmotnost 81 gramů.

Z porovnání je vidět, že první tryska bude výrobně nejnáročnější. Nejpracnější je dlouhý divergentní kužel a to vnitřní i vnější. U druhé trysky je právě tento kužel zkrácen a tím se snížila i hmotnost. Třetí tryska je minimalistická z hlediska pracnosti a délky polotovaru. Konvergentní kužel má zvětšený úhel, divergentní je velmi krátký a z vnější strany je nahrazen válcovou plochou. Naopak nedošlo k výraznému snížení hmotnosti. Dlužím ještě v_e, to je 1090 m/s.

Závěr si jistě uděláte sami. U malých motorů je obrazně téměř jedno, co tam bude za trysku. U velkých a hybridních už bych o propracovanější trysce uvažoval. A jak je vidět, dlouhá tryska nemusí být zákonitě přehnaně těžká. Spíš tu máme na vahách výkon a pracnost, v případě měděné trysky možná i cenu.

Mějte se,
Michal

Ahoj,

zatím jen krátce, spočítal jsem výtokovou rychlost pro A_e/A_t = 2,5. Je to 1165 m/s. Rozdíl je tedy cca 200 m/s tedy cca 18%. Tah motoru je dán vztahem F=m^{(s tečkou)} . v_e.

Michal

Ahoj Michale ,

díky za pěkný úvod do teorie trysek i za vzorový (ideální) výpočet.
Expanzní poměr Ae= 5,77 je však pro praktické použití dosti vysoký.

Taková tryska by byla podstatně delší než trysky běžne používané u našich SB reload motorů, tedy náročnější na výrobu ( v podstatě dvounásobná délka expanzní (divergentní ) části trysky, a také vyšší hmotnost trysky. Rozdíly v účinnosti trysky jsou spíše j jednotkách % , co je pro nás dost málo motivující. Daleko větší ztráty jsou jsou způsobeny v samotném návrhu motorů, jejich koncepci, kvalitě paliva a jeho laboraci v motoru a také v zážehu motoru.

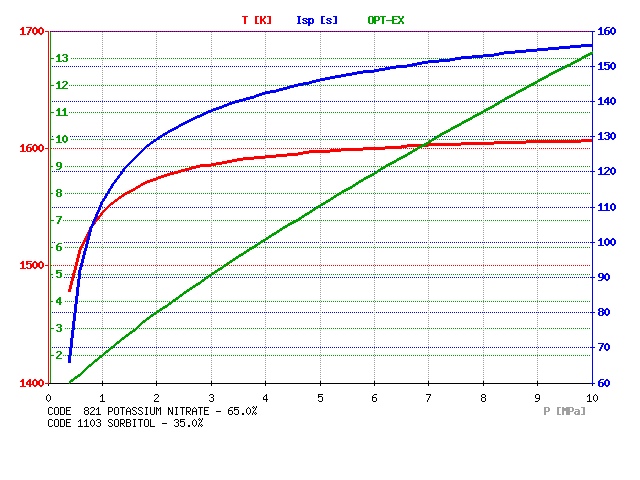
Podle diagramu pro sorbitolové palivo viď obr. v příloze vychází Ae pro tlak 3 Mpa necelých 5.

Pro ilustraci uvádím Expanzní poměr Ae pro několika u nás běžně používaných SB reload motorů (HP).

74 Ns Ae= 2,44 , 150 Ns Ae=2,3 , 340 Ns Ae=2,6 , 460 Ns Ae=2,32 , 800 Ns Ae= 2 !!

Už se těším na vášnivou debatu

Mirek

Geometrie trysky:
Tryska používaná u převážné většiny raketových motorů je tryska Lavalova z roku 1888 (Gustaf de Laval, 1845 - 1913)
Do té doby se nedařilo dosáhnout nadzvukového proudění plynů a kapalin. Zdánlivě logická úvaha, že zužování průřezu musí vést ke zvyšování rychlosti, v praxi nefungovala. Údajně náhodou a proto, že se panu Lavalovi líbila tryska, která se zužuje a následně rozšiřuje, dosáhl nadzvukového proudění. V krčku trysky je dosažena právě rychlost zvuku (Mach 1) a v navazující divergentní části dochází k expanzi, poklesu tlaku a dalšímu urychlování.
Ústí trysky má být navrženo tak, aby tlak expandujícího plynu byl roven tlaku okolí.
Tryska se tedy v podstatě skládá z konvergentní a divergentní části. Konvergentní část není krytickou částí trysky, lze použít různé tvary (různé úhly vstupního kuželu, různé velikosti rádiusů) bez podstatného vlivu na účinnost trysky.
Důležitou částí je část divergentní. Podstatná je rovněž kvalita povrchu trysky. Co se tedy týká divergentní části, používají se tyto dva základní tvary:
1. Kónická ( kuželová) tryska - nejstarší a nejjednoduší. Tzv. korekční faktor lambda, který ukazuje poměr hybnosti mezi danou tryskou a ideální tryskou, je dán úhlem výstupního kužele.
Zde několik hodnot:
alfa = 4 stupně

---

lambda = 0,9988
alfa = 10 stupňů --- lambda = 0,9924
alfa = 15 stupňů --- lambda = 0,9830
alfa = 20 stupňů --- lambda = 0,9698

Zhusta používaná tryska o úhlu 15 stupňů má tedy oproti ideální trysce 98,3 procentní účinnost.
S malým úhlem však velmi narůstá délka trysky a tedy i její hmotnost.

2. Zvonovitá tryska - u větších motorů nejpoužívanější. Má velký expanzní úhel hned za krčkem trysky, který plynule přechází do malého úhlu (zpravidla pod 10 stupňů) v ústí. Jako profil se často volí parabola. Tryska vychází kratší a lehčí než odpovídající kuželová tryska.

Pro naše účely se jednoznačně hodí více tryska kuželová.

Účelem výpočtu trysky je stanovit geometrii, která bude umožňovat co nejvyšší využití energie uvolněné spalováním paliva.
Protože tlak vzduchu se s rostoucí nadmořskou výškou snižuje, tryska bude mít optimální účinnost pouze v jediné výšce. Nad a pod touto výškou bude účinnost nižší.

Parametry trysky určují v podstatě dva rozměry:
Průměr D-krčku trysky a poměr Ae/At, tedy poměr průřezu na výstupu a průřezu v krčku - tzv. expanzní poměr.

Expanzní poměr Ae/At stanovíme z chemické analýzy hoření paliva, tlaku ve spalovací komoře a požadované výšky ideální expanze. Pro naše účely bude tato výška mezi 150 - 500 m n.m.

Průměr Dk určíme z požadovaného impulsu motoru.

Příklad 1: Sorbitolový motor o tahu 320N s dobou hoření 1,5 s (480Ns)
Předpokládáme konstantní průběh tahu po celou dobu hoření, tlak ve spalovací komoře 30 bar.

Lze to spočítat i ručně (viz kniha Rocket Propulsion Elements), my použijeme program RPA.

Tlak prostředí zvolíme 0,96 atm, což odpovídá nadmořské výšce 340 metrů.
První potřebná výstupní hodnota je Is. Zde dostáváme 1214 Ns/kg. Hmotnost paliva je tedy 395 g.
Hmotnostní průtok je tedy 263 g/s.

Použitím hodnoty pro Mass Flux (z RPA) tedy 3312 kg/m2s dostaneme plochu průřezu v krčku trysky:
At=0,794 cm2, a následně Dt=1 cm.

z RPA víme hodnotu Ae/At=5,77
Plocha Ae tedy bude 4,58 cm2 a De=2,42 cm

Některé další hodnoty:
Charakteristická rychlost c* = 884 m/s
Tahový koeficient CF=1.373
Teplota v krčku 1527 K
Teplota na výstupu 1155 K
Rychlost zvuku v krčku 590 m/s
Rychlost na výstupu z trysky 1372 m/s

Další příklady příště.
Mějte se,
Michal